حقائق عن المثلث {10}

{10}

المثلث

المثلث هو احد الاشكال الاساسية في الهندسة.و هو شكل ثنائي البعد مكون من ثلاثة رؤوس تصل بينها ثلاثة اضلاع، التي هي عبارة عن قطع مستقيمة.

انواع المثلثات
من الممكن تصنيف المثلثات تبعا لاطوال اضلاعها كما يلي:

· مثلث متساوي الأضلاع: وهو مثلث أضلاعه متساوية. جميع زوايا المثلث متساوي الاضلاع متساوية أيضا، وقيمتها 60 درجة.
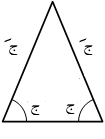
· مثلث متساوي الساقين: وهو مثلث فيه ضلعان متساويان. الزاويتان المقابلتان لهذين الضلعين تكونان متساويتان أيضا.
· مثلث مختلف الأضلاع: وهو مثلث أطوال أضلاعه مختلفة. زوايا هذا المثلث تكون مختلفة القيم أيضا.

1-متساوي الأضلاع 2-متساوي الساقين 3- مختلف الاضلاع

كما يمكن تصنيف المثلثات تبعا لقياس أكبر زاوية في المثلث:

· مثلث قائم: له زاوية قياسها 90 درجة (زاوية قائمة)، يدعى الضلع المقابل للزاوية القائمة بالوتر، وهو أطول أضلاع هذا المثلث.
· مثلث منفرج الزاوية: له زاوية قياسها أكبر من 90 درجة (زاوية منفرجة).
· مثلث حاد الزوايا: كل زواياه قياسها أصغر من 90 درجة (زاوية حادة).

1- قائم 2- منفرج 3- حاد

------------------------------------------------------------------------------------------------------------------------------------------------------

حقائق عن المثلثات

------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

تشابه مثلثين

يقال عن مثلثين انهما متشابهين اذا كانت الزوايا المتقابلة من كل منهما متساوية، اي عندما ينتج احدهما عن الاخر بتكبيره او تصغيره.

ان اطوال اضلاع المثلثين المتشابهين متناسبة، اي انه اذا كان طول اقصر اضلاع المثلث الاول هو ضعفا طول اقصر اضلاع المثلث الثاني، فان طول كل من الضلعين الاطول و المتوسط من المثلث الاول هو ضعفا طولي لضلعين الاطول و المتوسط من المثلث الثاني ايضا، و بالتالي فان النسبة بين طولي الضلعين الاقصر و الاطول في المثلث الاول مساوية للنسبة بين طولي الضلعين الاقصر و الاطول في المثلث الثاني.

نظرية فيثاغورس

واحدة من النظريات الاساسية في المثلثات هي نظرية فيثاغورث و التي تنص على انه في المثلث القائم، مربع طول الوتر (ا َ) يساوي الى مجموع مربعي طولي الضلعين القائمين (ب َ، ج َ)، اي:
د َ² = ب َ² + ج َ²
مما يعني ان معرفة طولي ضلعين من المثلث القائم، كاف لمعرفة طول الضلع الثالث:
من الممكن تعميم نظرية فيثاغورث لتشمل اي مثلث عبر قانون التجيب:
د َ² = ب َ² + ج َ² - 2 ب َ ج َ تجب د
و هو صحيح من اجل كل المثلثات حتى و لو لم تكن د قائمة.
مساحة المثلث
تعطى مساحة المثلث بالقانون:
سط = ق × ع / 2
حيث ان ق هي طول احدى اضلاع المثلث (القاعدة)، و ع هو طول العمود النازل على هذا الضلع من الرأس المقابل له (الارتفاع).
من الممكن البرهان على ذلك من خلال الشكل التالي:

الاهداف العامة لتدريس الرياضيات {9}

{9}

الاهداف العامة لتدريس الرياضيات

ان الاهداف التي سنذكرها هنا تكون لجميع المستويات ابتداء من المرحلة الابتدائية حتى المرحلة الجامعية كمثال على ذلك المفهوم الرياضي مثلا يمكن ان يدرس في اكثر من صف من الصفوف المتتالية وقد يمتد الى اكثر من مرحلة ولكن معالجته في الصفوف العليا يكون اكثر عمقا فعلى سبيل المثال يمكن معالجة مفهوم التفكير الاستقرائي ومفهوم التفكير الاستدلالي بالمرحلة الابتدائية من خلال امثلة لكل منها ثم يدرس نفس المفهومين بعد ذلك في المراحل التالية بشئ من التفصيل واكثر دقة وشموليه ويمكن تحديد اهم الاهداف العامة لتدريس الرياضيات كما يلي ...

اتاحة الفرصة لممارسة طرق التفكير السليمة

يستخدم الطالب اساليب تفكير مختلفه مثل الاستقرائي والاستدلالي والتأملي
يعرف حدود الثقة في النتائج التي يحصل عليها عن طريق احد اساليب التفكير
يعرف الفرق بين القضايا المطلقة التعميم وتلك المحدودة التعميم
يحاول التأكد من صحة القضايا التي يعتمد عليها في اتخاذ القرار
يحاول مراجعة خطوات تفكيره في ضوء القضايا المعطاة والموثوق فيها

اكتساب المهارة في حل المشكلات الرياضية

يحدد معاني الالفاظ والرموز الوارة في نص المشكلة ويتعرف على العلاقات المتضمنه
يحدد مالمطلوب في المشكلة والمعلومات التي سيعتمد عليها في الحل
يترجم المشكلة الى علاقات او اشكال هندسية
يفترض الافتراضات الممكنة للحل
يحدد المعلومات الناقصة والتي قد تؤدي الى حل المشكلة
يصل الى الحل بصياغة علمية منطقية ويدعم خطواته اكثر
يراجع الحل ويتأكد من صحته
يحاول البحث عن اكثر من طريقة لحل المشكلة
يجيد صياغة المشكلة المعطاة بصورة افضل
يحاول الاستفادة من حل مشكلة مماثلة
يقترح مشكلة من ابداعه او يطور المشكلة التي حلها

التعرف على اثر الرياضيات واهميتها في تطوير المجتمع

يتعرف على اهم جوانب تاريخ الفكر الرياضي وبخاصة عند المسلمين
يتعرف على اهم جوانب تفاعل الرياضيات مع حضارة الانسان
يتعرف على اهم مجالات تطبيق الرياضيات في بيئته المحلية
يتعرف على مهام الرياضيات في خدمة العلوم الاخرى
يلم باهم وظائف الرياضيات في التقدم العلمي
يحاول استخدام الرياضيات في مجالات حياته العامة

اكتساب المهارات اللازمة للاستيعاب والكشف عن علاقات جديدة

يجيد قراءة المشكلة ويفسر ما فيها من الفاظ ورموز

تمثيل العلاقات باشكال هندسية او وسائل تعليمية اخرى

تذكر المعلومات بسرعة

اسناد جميع خطوات الحل الى اسسها الرياضيه

استنتاج علاقات جديدة لتوضيفها

يكون فكرة صحيحة عن الجواب اما عن طريق التخمين او الحدس

يحصل على الاجابة في اقل وقت ممكن

يستخدم طرائق مختلفة في حل المشكلة

تكوين ميول واتجاهات سليمة نحو الرياضيات

الحث على حضور دروس ارياضيات واحترام المعلم

تأدية جميع الواجبات وبشكل صحيح وفي الوقت المحدد

يكثر من الاستفسار عن الجديد من الافكار الرياضية واستنتاج البعض بنفسه

يحاول البحث عن اكثر من حل للمشكلة وحل مشكلات كثبره

يحاول المزيد من القراءة عن الرياضيات وبعمق اكثرومن مصادر اخرى خلاف المنهج الدراسي

يحاول تفسير بعض الظواهر ويتعرف على اثر الرياضيات فيها وفي تطوير الفكر البشري

يهوى الكشف عن النماذج الرياضية ويجب ويغرم بها





الاعتماد على النفس في تحصيل الرياضيات

ينصت بحرص للمناقشات ويسجل الافكار الرئيسية للدرس

يجيد تلخيص كل ما تقع عليه عيناه عن الرياضيات

يستطيع اعداد خطة لتنظيم وقته لاستذكار مختلف المواد

تكوين المهرة في كتابة حلول منظمة ودقيقة من الناحية المنطقية

التعرف على مصادر المعلومات من خارج الكتب المدرسية

يحاول مناقشة مالايستطيع حله مع الغير

يستطيع حل التمارين بدون مساعدة المعلم ويتقدم عليه في حل تمارين الكتاب

يكثر من التمارين الخارجه عن تمارين الكتاب لمناقشتها مع المعلم

تكوين عاداة مرغوب فيها وتقبل النقد

يتبادل المعلومات مع غيره من الطلبة ومساعدة من يحتاج

يحافظ على سلامة ونظافة كتبه وادواته وينظم الكتابة في دفتر الرياضيات

لا يقاطع زميله في المناقشة ويتقبل النقد من مدرس الرياضيات ومن زملائه

يتوخى الدقة في رسم الاشكال الهندسية وفي التعبير عن الرموز

يقبل على الاعمال الجماعية او التطوعية

انتهى ...

علماء الرياضيات {8}

{8}

علماء الرياضيات

ابن الهائم (753-815 هـ / 1350 -1412 م) أبو العباس شهاب الدين أحمد بن محمد بن عماد الدين بن علي المعروف بابن الهائم المصري المقدسي ، رياضي وعالم فرائض اشتهر في القرن الثامن الهجري / الرابع عشر الميلادي. ولد بالقاهرة ، وفيها حفظ القرآن ودرس مبادئ العلم الأولى. وعندما بلغ سن الشباب غادر إلى القدس وفيها أقام بقية عمره، ومنها جاء نسبه المقدسي. قام ابن الهائم بعد استقراره في القدس بتدريس علم الرياضيات وعلوم الشريعة لطلاب العلم، فاشتهر بذلك وعلا شأنه وأصبح من أبرز علماء الرياضيات في العالم الإسلامي. ولعل أهم ما ميز ابن الهائم هو طريقته في التدريس التي أسسها على تقوى الله، فكثيرا ما كان يحث طلابه أن يكونوا قدوة حسنة في العمل الجاد والتمسك بدينهم الحنيف. فلقبه الناس بالمعلم، فأحبه تلاميذه وقدروه وحاولوا تقليده. ولقد كان ابن الهائم يقضي نهاره في التدريس، ثم ينتقل بعد ذلك إلى المسجد الأقصى فكان يقضي وقته هناك يعظ الناس ويأمرهم بالمعروف وينهاهم عن المنكر، ويفقههم في الدين حتى صار من كبار فقهاء الإسلام في الدعوة والإرشاد والإفتاء.

وقد كان لاهتمام ابن الهائم بعلوم الشريعة أثر كبير في توجيهه علم الرياضيات لخدمة الدين، فاهتم اهتماما بالغا بعلم الفرائض ومسائل حساب الميراث وتوزيع التركات حتى أصبح أعلم أهل زمانه في هذا العلم لدرجة أنه عرف بالفرضي ،وما زال ابن الهائم على هذه الحال حتى وافته المنية عام 815هـ / 1412 م. عن عمر يناهز اثنين وستين عاما.

وتتجلى شهرة ابن الهائم في علم الحساب أنه ابتكر طرقا مبسطة لعمليات ضرب الأعداد (فمثلا يكون ضرب أي عدد في خمسة عشر بجمع نصف قيمة ذلك العدد إليه ثم الضرب في عشرة). ولقد أودع هذه الطريقة في كتابه المعروف باسم اللمع في الحساب وهي رسالة تجمع بين العلم والأدب وقد قام بشرحها تلميذه سبط المارديني.

كما ترك ابن الهائم عددا آخر من المؤلفات كان معظمها في علم الحساب والجبر والفرائض من أهمها: كتابه أسنان المفتاح وهي ملخص لكتابه المعونة في الحساب الهوائي ، وله في الحساب الهوائي أيضا كتاب مختصر في علم الحساب المفتوح الهوائي ، ومن كتبه أيضا كتاب الحاوي في الحساب ، وكتاب /1 2 مرشدة الطالب إلى أسنى المطالب وقد شرح هذا الكتاب الشيخ عبدالله الشنشوري. ومن مؤلفاته في الجبر كتاب المقنع في الجبر والمقابلة ، وقد قام بنظمه في قصيدة لامية من حوالي ستين بيتا شرحها في رسالة بعنوان المسمع في شرح المقنع . كما له شرح الأرجوزة الياسمينية لابن الياسمين في الجبر. ومن أعماله في الفرائض كتاب غاية السول في الإقرار بالدين المجهول ، ورسالة التحفة المقدسية /12 وهي نظم في كيفية حساب الإرث. الخوارزمي (164-232هـ / 781 -850م)

كتاب الزيج للخوارزمي

تنقيح المجريطي أبو عبد الله محمد بن موسى الخوارزمي، أحد أشهر علماء الرياضيات والفلك والجغرافية الذين اشتهروا في القرن الثالث / التاسع الميلادي الهجري. ولد في بلدة خيوق جنوب إقليم خوارزم (أوزبكستان حاليا)، ثم انتقل إلى بغداد حيث ولاه المأمون منصبا في بيت الحكمة فعمل على جمع الكتب اليونانية.

وقد جرى الخوارزمي على العكوف في مكتبة المأمون للدرس.

ومن ثم فإن الخوارزمي اعتمد فيما بلغ إليه من شأو في الجبر على الهند والفرس ومدرسة جنديسابور على وجه الخصوص . كما انصرف الخوارزمي إلى دراسة الرياضيات والجغرافية والفلك والتاريخ. فألف كتبه قبل العصر الذي ازدهر فيه النقل عن العلوم اليونانية.

عاش الخوارزمي في عهد المأمون وكان أحد منجميه، وقد اشترك في حساب ميلان الشمس في ذلك العهد. وتناول الخوارزمي أيضا مسائل في التنجيم من الناحية العملية. وبحث إلى أي حد نبأ اقتران الكواكب عند مولد النبي صلى الله عليه وسلم برسالته، كما أعد الخوارزمي أيضا مجموعة من صور السموات والعالم نزولا على إشارة المأمون. وتعود شهرة الخوارزمي الحقيقية إلى أنه أول من ابتكر علم الجبر وفصله عن علم الحساب. فظل في مقدمة العلوم الرياضية طوال ثلاثة قرون متتالية. فقد بين الخوارزمي معادلات الدرجة الثانية بأنواعها الثلاثة من الحدود معرفا الجذر (س) والمال (س2) والعدد المفرد (الحد الخالي من س). وقد بدأ بذكر المعادلات التي تحتوي على حدين اثنين من هذه الحدود، فعدد أشكالها الثلاثة على الترتيب:أ س = ب س، أ س2 = حـ، ب س = حـ.

وشرح طريقة حل كل منها بأمثلة عددية مقتصرا على الكميات الموجبة المحددة. وقد استطاع الخوارزمي التأليف بين الرياضيات الإغريقية والهندية، ومن الهندية أدخل نظام الأرقام بدلا من الحروف الأبجدية. كما أدخل على الأعداد النظام العشري، واستخدم الصفر .

ومن أهم أعماله أيضا أنه وضع جداول الجيوب في المثلثات، والتمثيل الهندسي للمقاطع المخروطية وتطوير علم حساب الخطأين الذي قاده إلى مفهوم التفاضل. كما قدم الخوارزمي إسهامات في الجغرافية والخرائط الجغرافية. وكتب عن المزاول و الساعات و الأسطرلابات. ولقد أثر الخوارزمي في الحضارة الغربية كثيرا، حتى ارتبط اسمه الخوارزمي بمصطلح "الخوارزميات" ويعني أحكام خطوات حل المسائل الرياضية. وقد عرف هذا المصطلح في اللغات الأوروبية بـ Algorithim . كما كان له الفضل لدخول كلمات أخرى مثل الجبر Algebra والصفر Zero إلى اللغات اللاتينية. ترك الخوارزمي عددا من المؤلفات في شتى المعارف من أهمها كتاب الجبر والمقابلة وهو أهم كتبه، وكتاب الجمع والتفريق في الحساب الهندي ، وكتاب رسم الربع المعمور ، وكتاب تقويم البلدان ، وكتاب العمل بالأسطرلاب ، وكتاب التاريخ .

الكافي في الحساب {7}

{7}

الكافي في الحساب


أحد أهم وأشهر الكتب التي ألفت في علم الحساب في القرن الخامس الهجري / الحادي عشر الميلادي.

أراد به مصنفه أبو بكر محمد بن الحسن الكرجي أن يخصصه للموظفين ولعامة الناس ولمن يود حساب الزكاة والوصايا أي أنه مخصص للحساب العملي وليس النظري. ولعل هذا هو السبب الذي جعل الكتاب يستخدم أسلوب حساب اليد الذي كانت تستخدم فيه الأصابع.

ويشير الكرجي إلى سبب تأليفه لهذا الكتاب فيقول: "معاشر إخواني أيدكم الله بفضله وأعانكم على طاعته قد طال تقاضيكم بالمختصر الذي سألني تصنيفه شرف أهل الفضل الأستاذ الجليل أبو الحسن أحمد بن علي البتي أدام الله تأييده وطالت مدافعتي به لعوائق اتصلت وموانع ترادفت، وها أنا قد جئت به الآن صفوا بلا حشو، على المثال الذي مثله والحد الذي رسمه ضامنا لما يحتاج إليه الناس، على طبقاتهم في جميع معاملاتهم على اختلافها، شاكرا لنعم الله المتواصلة، وآلائه المتظاهرة ومصليا على محمد نبيه ورسوله وآله أجمعين".

محتويات الكتاب
يبدأ الكتاب بمقدمة بسيطة يذكر فيها السبب الذي بعث الكرجي على تأليف هذا الكتاب كما يقرر أنه مختصر خال من التطويل والحشو، ثم بعد ذلك يأخذ في ذكر أبواب الكتاب وهي تقع في (69) بابا يمكن أن نلخصها فيما يلي:
أبواب الضرب: وتشمل باب الضرب للصحاح ثم باب في ضرب الأعداد المركبة وتلي هذا الباب ستة أبواب أخرى متنوعة في الضرب، ولعل السبب في ابتداء الكتاب بأبواب الضرب أن كتب حساب اليد كانت تهمل الجمع والضرب باعتبارهما عمليتين سهلتين فكانت تبدأ في العادة بفكرة المراتب ومنها تنتقل إلى الضرب والقسمة، والقسمة تؤدي إلى الكسور والنسبة ثم تطبيق هذه المبادئ في مسائل المعاملات والمساحة مع ذكر لمبادئ الجبر والاستعانة به في حل المجهول.

أبواب الكسور: وتشمل الكسور ومخارجها، ثم الحديث عن النسبة وفيها يتكلم عن النسبة إلى الصحاح، ويذكر ملخصا لعبارات النسبة، ثم يذكر نسبة الكسور والنسبة إلى الستين والكسور المضافة، ثم يخصص بابا يذكر فيه مسائل من نسبة الكسور المفردة مع الصحاح إلى الستين وبابا آخر باسم مسائل من النسبة، ثم يتكلم عن النسبة إلى الأعداد المشتركة والأوائل، ثم ضرب الكسور مفردة وغير مفردة.

أبواب القسمة: ويشم ل قسمة ما يكون فيه كسور، وقسمة الدرج وأجزائها، ثم يذكر بابا في التحويلات واستخراج الجذور وأخذ جذور المقادير التي معها كسور.

أبواب المساحات: وتشمل أبوابا في المثلثات، والدائرة وقطاعاتها ومساحة ذوات الأضلاع الكثيرة، ثم يتكلم عن مساحة السطوح، ومساحة المجسمات ومعرفة وزن الأرض .
أبواب المسائل الجبرية: وتشمل أبواب الحساب من الضرب، والقسمة، والنسبة، والجمع، والتفريق، والجبر والمقابلة.
أبواب النوادر: وتشمل أبواب في المسائل المقترنة بالنوادر والمسائل ونوادر المساحة.

النسخ المحققة
حقق الكتاب سامي شهلوب ونشره معهد التراث العلمي العربي التابع لجامعة حلب ضمن مصادر ودراسات في تاريخ الرياضيات العربية رقم (5)، عام 1406هـ / 1986 م.

انتهى ....

ملخص لهندسة الدائرة والمثلثات {6}

{6}

ملخص لهندسة الدائرة والمثلثات

1) إذا تساوت الأوتار ( أ حـ = هـ حـ) فإن:

1) تساوت الزوايا المحيطية المرسومة على أقواسها.
ق< ب = ق< د

2)تساوت الزوايا المركزية المرسومة على أقواسها.
ق.<أ م حـ = ق<هـ م حـ

3) تساوي أبعادها عن المركز.
م و = م ن


4) تساوت أقواسها. القوس أ ل حـ = القوس هـ ك حـ


لدينا هنا خمسة : وتر، قوس، زاوية محيطية، زاوية مركزية، بعد


تحقق أي منها يتحقق الأربع الآخرون.

* الزاوية المركزية تساوي ضعف الزاوية المحيطية المشتركة معها في نفس القوس

2) ل ن مماس للدائرة م فإن م ن (نصف القطر) يكون عمودياً على المماس ل ن أي: م ن ^ ل ن

3) حـ د وتراً في الدائرة م ، م هـ^ حـ د فإن هـ منتصف حـ د والعكس صحيح أي:

هـ منتصف حـ د فإن م هـ^ حـ د
4) أ ب قطراً في الدائرة م فإن ق<(أ ك ب) = 90^ه


5) ل ن مماس للدائرة م، ل س ك قاطع للدائرة م فإن: (ل ن)² = ل س × ل ك


6) تسمى زاوية أم ن مركزية والزاوية أ ك س بالمحيطية



7) أي مستقيم في مستوى الدائرة أما أن:


يقطع الدائرة في نقطيتين فهو وتر


يقطع الدائرة في نقطة فهو مماس


لا يقطع الدائرة فهو خارجها




8) أي نقطة في مستوى الدائرة أما أن:

تكون داخلها فيكون بعدها عن المركز أقل من نصف قطر الدائرة
تكون على محيطها فيكون بعدها عن المركز يساوي نصف قطر الدائرة
تكون خارجها فيكون بعدها عن المركز أكبر من نصف قطر الدائرة


9) أي ثلاث نقط ليست على استقامة واحدة تمر بها محيطة دائرة واحدة فقط

---

10) المستقيم العمودي على نصف قطر الدائرة عند نهايته يكون مماساً للدائرة.


أ ب ^ نق ( أ م )


11) لا يمكن رسم سوى مماس واحد فقط من نقطة على محيط الدائرة.


مثل المماس أ ب


12) العمود المقام على المماس من نقطة تماسه مع الدائرة يمر بمركز الدائرة مثل أ م

13) العمود النازل من مركز الدائرة على المماس يمر بنقطة التماس.


أ م عمودي على المماس أ ب عند نقطة أ



14) إذا رسم مماسان من نقطة خارج الدائرة فإن:


أ) المماسان متساويان ( ل ك = ل ن )



ب) يحصران عند المركز زاويتان متساويتان (< ل م ك = < ل م ن )

ج) يميلان بزاويتين متساويتين على المستقيم الواصل من النقطة لمركز الدائرة ( < م ل ك = < م ل ن )



15) الزاوية المحصورة بين المماس والوتر تساوي الزاوية المحيطية المرسومة على الوتروالعكس صحي
< ب أ ص = < أ س ص


16) إذا تماس محيطا دائرتين فإن نقطة التماس تقع على خط المركزين


17) إذا كانت الدائرتان متماستان من الخارج فإن البعد بين المركزين يساوي مجموع نصفي قطريهما.

18) إذا كانت الدائرتان متماستان من الداخل فإن البعد بين المركزين يساوي الفرق بين نصفي قطريهما

19) المماس المشترك لدائرتين هو المار المستقيم المار بنقطة تماسهما

20) المماس المشترك لدائرتين يكون عمودياً على خط المركزين.


21) المماسان المرسومان من نقطة واحدة للدائرة متساويان و أ = و هـ


22) الزاوية المحصورة بين المماس والوتر تساوي الزاوية المحيطية المرسومةعلى هذا
الوتر ق<(و أ ب) = <(أ حـ ب)



23) في الشكل الرباعي الدائري أ ب حـ د يكون:


أب × حـ د + ب حـ × أ د = أ حـ × ب د
كل زاويتين متقابلتين مجموعهم 180^ه والعكس صحيح


24) الزوايا المحيطية المرسومة على قوس واحد متساوية


25) المماسان المرسومان من طرفي قطر للدائرة متوازيان


26) المستقيم الواصل من نقطة و لمركز الدائرة ينصف زاوية و


27) في المثلث القائم إذا أنزل عمود من رأس القائمة على الوتر فإن


مربع العمود = حاصل ضرب جزئي الوترأ قائمة ، أ د عمودي علي ب حـ ( أ د )² = ب د × حـ د ، ( أ ب )² = ب د × ب حـ ، ( أ حـ )² = حـ د × حـ ب

حساب المثلثات

فرع من فروع الرياضيات يعالج العلاقات بين أضلاع وزوايا المثلثات والخصائص
والتطبيقات العملية للدوال المثلثية، وينقسم حساب المثلثات إلى فرعين: حساب
المثلثات المستوية ويتعامل مع أشكال تقع بأكملها في مستوى واحد وحساب المثلثات الكروية
ويتعامل مع المثلثات التي تعتبر جزءا أو مقطعا من سطح كرة.

وقد كانت أولى التطبيقات العملية لحساب المثلثات في مجالات الملاحة والمساحة والفلك حيث كانت المشكلة
الكبرى في كل هذه المجالات تحديد مسافة غير معلومة مثل المسافة بين الأرض والقمر
أو مسافة لا يمكن حسابها بصورة مباشرة مثل المسافة التي تغطي بحيرة كبيرة. ومن بين
التطبيقات العملية الأخرى لحساب المثلثات استخدام هذا العلم في الفيزياء والكيمياء وكل فروع

الهندسة تقريبا خاصة في دراسة الظواهر المتكررة مثل الموجات الصوتية
أو تدفق تيار متناوب.

وتعرف الدوال الستة المثلثية الأكثر استخداما على النحو التالي:

جا أ = ر / س، جتا أ = ر / ص ، ظا أ = س / ص
ظتا أ= ص / س، قا أ = س / ر،قتا أ = ص / ر

حيث أن (ر) وتر المثلث وكل من (س) و(ص) ضلعيه، وأن ر2 = س2 + ص2
حسب نظرية فيثاغورس للمثلث القائم الزاوية. وأن (س) و(ص) لا يتغيران إذا أضيفت
الزوايا الدائرية (2 ط) على الزاوية، بمعنى أنه إذا أضيف 360ْ إلى الزاوية فإن جا
(أ + 2 ط) = جا أ ، وهناك عبارات أخرى تنطبق على الدوال الخمس الأخرى.

وتعتبر ثلاثة من هذه الدوال عكس الثلاثة الأخرى بمعنى أن:

ظتا أ = ظا أ / 1 ، قا أ = جتا أ / 1 ، قتا أ = جا أ / 1

وإذا كانت أ، ب، ج هي الزوايا الثلاثة لمثلث،
وكانت س ص ع هي الأضلاع المقابلة الخاصة بكل من هذه الزوايا، بالتالي يمكن إثبات أن:

جا أ / س = جا أ / ص = جا أ / ع

ويمكن أن تأخذ قوانين جيب التمام (جتا) والمماسات أشكالا أخرى بالتناوب بين الحروف الزوايا (أ ب ج) والأضلاع (س ص ع).

ويمكن استخدام هذه العلاقات الثلاثة في حل أي مثلث بمعنى أنه يمكن الوصول إلى
الزوايا أوالأضلاع المجهولة عند معرفة: ضلع واحد وزاويتين، أو الضلعين والزاوية
المحصورة بينهما، أو ضلعين وزاوية مقابل أي منهما (عادة ما يكون هنالك مثلثان في هذه الحالة) أو كل الأضلاع الثلاثة.

نبذة تاريخية

يعود تاريخ حساب المثلثات إلى أقدم ما
دون عن الرياضيات في مصر وبابل، حيث قاس البابليون الزوايا بالدرجات والدقائق
والثواني. وحتى عصر اليونانيين، لم يوجد أي تطور ملحوظ في حساب المثلثات،
وفي القرن الثاني قبل الميلاد، وضع الفلكي هيباركوس جدول مثلثي لحل المثلثات، حيث
بدأ بــ 7.5ْ حتى وصل إلى 180ْ بدرجات مقدارها 7.5ْ، وقد أعطى الجدول لكل زاوية طول
الوتر المقابل لهذه الزاوية في دائرة ذات نصف قطر ثابت ر. ومثل هذا الجدول مكافئ
لجدول الجيب ، ولم تكن القيمة التي استخدمها هيباركوس لنصف القطر (ر) محددة، ولكن
بعد مضي 300 عام استخدم الفلكي بطليموس (ر)= 60 لأن اليونانيين قد أخذوا نظام
الأرقام الستينية

وقد ذكر بطليموس في كتابه المجسطي جدول أوتار لدرجات النصف من
صفر إلى 180ْ وهي تعادل (3600 / 1 ) من الوحدة، كما أنه قد شرح أيضا طريقة عمله
لجدول الأوتار هذا، وفي عرضه للكتاب ذكر أمثلة عديدة على كيفية استخدام الجدول للتوصل
إلى الأجزاء المجهولة من المثلثات من خلال الأجزاء المعروفة، وقد ذكر بطليموس
ما يعرف الآن باسم نظرية مينيلوس لحل المثلثات الكروية، ولقرون عديدة كان ما دونه
بطليموس في حساب المثلثات المقدمة الأساسية للموضوعات التي يتناولها أي
فلكي.


وفي نفس عصر بطليموس تقريبا، طور الهنود نظاما لحساب المثلثات يعتمد على دالة
الجيب وليس على دالة الوتر التي اعتمد عليها اليونانيون، وعلى عكس الدالة الحديثة،
لم تكن دالة الجيب هذه نسبة وإنما كانت ببساطة طول الضلع المقابل للزاوية في مثلث
قائم الزوايا ذي وتر ثابت محدد، هذا وقد استخدم الهنود قيما متعددة لوتر المثلث
القائم الزاوية.


وفي نهاية القرن الثاني الهجري / الثامن الميلادي، ورث
الفلكيون المسلمون التراث اليوناني والهندي واستخدموا دالة الجيب، وبحلول نهاية
القرن الرابع الهجري / العاشر الميلادي، كانوا قد أكملوا الجيب والدوال الخمس الأخرى،
كما وضعوا العديد من النظريات الأساسية في حساب المثلثات تتعلق بكل من المثلثات
المستوية والكروية.

فقد رأى البيروني أن
الفترات المتساوية بين الزوايا لا تقابلها تغيرات متساوية في النسب المثلثية ، فأثبت
صحتها بالطرق الهندسية، وقام بعمل جداول للجيب لكل ربع درجة بدلا من الجداول
المعروفة آنذاك، وقد قام بإيجاد طول الوتر في دائرة يقابل زواية قدرها 40ْ عند
المركز، وكان هدفه إيجاد الأوتار التي تقابل من الدورة الكاملة ثلثها وربعها
وخمسها، وقد تمكن من استنتاج قوانين مبسطة لحساب قيم هذه الأوتار فيما عدا وتري
السبع والتسع، كما استنتج قوانين لوتر مجموع زاويتين أو الفرق بينهما أو قيمة نصف
الزاوية مستخدما طريقة التقريب المتتابع.


ثم طور الطوسي من نظريات جيب
الزاوية إلى ما هي عليه الآن مستعملا المثلث المستوي، وعمل في ذلك الجداول
الرياضية له ، كما قدم قاعدة الأشكال المتتامة وهي الصورة المبسطة لقانون
الجيوب الذي يقضي بأن جيوب الزوايا تتناسب مع الأضلاع المقابلة لها.

أما الكاشي فقد حسب جداول
جيب الدرجة الأولى، واستخدم ذلك في معادلة ذات الدرجة الثالثة في معادلاته
المثلثية ويقول في ذلك: " إذا علم جيب قوس، وأريد معرفة جيب ثلاثة
أمثالها، يضرب مكعب ذلك الجيب في أربع ثوان، وينقص الحاصل من ثلاثة أمثاله، فالباقي
هو الجيب المطلوب" وصورة ذلك على مايلي:


(جا 3س = 4جا س2 - 3جا س).


كما توصل المسلمون أيضا إلى المثلث القطبي للمثلثات الكروية، وقد طبقت كل هذه
الاكتشافات في أغراض فلكية، واستخدمت كوسيلة مساعدة في حساب الوقت فلكيا، وفي التوصل إلى اتجاه


مكة المكرمة لأداء الصلوات الخمس التي فرضتها الشريعة الإسلامية، كما توصل العلماء
المسلمون إلى جداول ذات دقة عالية، فعلى سبيل المثال الجداول التي وضعوها للجيب والمماس
كانت دقيقة جدا بنسبة أكبر من جزء واحد من 700 مليون.


وقد اهتم الطوسي بعلم حساب المثلثات الكروية اهتماما بالغا ووصل فيها شأوا، فكان أول من قدم
المتطابقات المثلثية للمثلث الكروي قائم الزاوية. أما


ابن يونس فقد ابتكر القانون المعروف في حساب المثلثات (جتا أ جتا ب =2 / 1 [ جتا (أ + ب ) + جتا ( أ- ب)])


الذي يقضي بتحويل عملية الضرب إلى عملية جمع، فكان بذلك واضعا أول حجر في تطوير علم


اللوغاريتمات.

ولقد اشتغل البتانيبالأعمال الفلكية الموجهة إلى حساب المثلثات، وكان يستخدم الجيوب بانتظ ام مع يقين واضح من
تفوقها على الأوتار التي استعملها الإغريق من قبل. وقد أكمل إدخال دوال الظل وظل التمام، وعمل جدولا لظل التمام بدلالة الدرجات على أساس العلاقة (ظتا أ = جتا أ / جا أ). كما عرف العلاقة بين الأضلاع والزوايا في المثلث الكروي العام والتي يعبر عنها بالمعادلة

(جتا أ = جتاب. جتا جـ + جا ب. جا جـ).

وبعد ذلك، تعرف الغرب على ما صاغه المسلمون في علم حساب المثلثات من خلال ترجمة كتب الفلك العربية وقد بدأت
حركة الترجمة في القرن الثاني عشر، وقد كان أول عمل غربي يكتب في هذا
الموضوع من تأليف الفلكي والرياضي الألماني يوهان مولر وقد سمى كتابه ريجيو مونتانوس .

وفي القرن التالي، توصل الفلكي الألماني جورج يوأخيم المعروف باسم
ريتيكس إلى المفهوم الحديث لدوال حساب المثلثات على أنها نسب وليست أطوال خطوط
معينة. أما الرياضي الفرنسي فرانسوا فيتي فقد أدخل المثلث القطبي في حساب المثلثات
الكروية وقد ذكر الصيغ المتعددة الزوايا للجيب وجيب التمام من خلال قدرة الجيب وجيب التمام.


وقد خطا حساب المثلثات خطوات كبيرة إلى الأمام في أوائل القرن السابع عشر على
يد عالم الرياضيات الأسكتلندي جون نابير الذي اخترع اللوغاريتمات، كما
اخترع أيضا بعض القوانين المساعدة للذاكرة لحل المثلثات الكروية وكذا بعض النسب لحل
المثلثات الكروية المائلة.


وبعد نصف قرن تقريبا من نشر نابير للوغاريتمات التي
وضع أسسها ابن يونس، توصل إسحاق نيوتن إلى حساب التفاضل والتكامل. وكان من ضمن
الأساسيات التي اعتمد عليها هذا العمل تقديم نيوتن للعديد من الدالات على أنها
متسلسلات لا نهائية في قدرات (س). ومن ثم فقد توصل نيوتن إلى متسلسلة الجيب (س)
ومتسلسلة مماثلة لجيب التمام (س) وظا (س). ومع اختراع حساب التفاضل والتكامل، أعيد
النظر في تحليل الدوال المثلثية حيث ما زالت تلعب دورا هاما في كل من الرياضيات
البحتة والتطبيقية.


وأخيرا، وفي القرن الثامن عشر، عرف الرياضي السويسري
ليونهارد يولر الدوال المثلثية على أنها أعداد مركبة، وقد أدى هذا إلى أن جعل مادة
حساب المثلثات بأكملها تطبيقا واحدا من التطبيقات العملية الكثيرة للأعداد المركبة،
وأظهر أن القوانين الأساسية للرياضيات مجرد نتائج لحساب هذه الأعداد.

إنتهى ...

حساب المثلثات {5}

{5}

حساب المثلثات

فرع من فروع الرياضيات يعالج العلاقات بين أضلاع وزوايا المثلثات والخصائص
والتطبيقات العملية للدوال المثلثية، وينقسم حساب المثلثات إلى فرعين: حساب
المثلثات المستوية ويتعامل مع أشكال تقع بأكملها في مستوى واحد وحساب المثلثات
الكروية ويتعامل مع المثلثات التي تعتبر جزءا أو مقطعا من سطح كرة.

وقد كانت أولى التطبيقات العملية لحساب المثلثات في مجالات الملاحة والمساحة
والفلك حيث كانت المشكلة الكبرى في كل هذه المجالات تحديد مسافة غير معلومة مثل
المسافة بين الأرض و القمر أو مسافة لا يمكن حسابها بصورة مباشرة مثل المسافة التي
تغطي بحيرة كبيرة. ومن بين التطبيقات العملية الأخرى لحساب المثلثات استخدام هذا
العلم في الفيزياء والكيمياء وكل فروع الهندسة تقريبا خاصة في دراسة الظواهر
المتكررة مثل الموجات الصوتية أو تدفق تيار متناوب.

وتعرف الدوال الستة المثلثية الأكثر استخداما على النحو التالي:
جا أ = ر / س، جتا أ = ر / ص ، ظا أ = س / ص
ظتا أ= ص / س، قا أ = س / ر، قتا أ = ص / ر
حيث أن (ر) وتر المثلث وكل من (س) و(ص) ضلعيه، وأن ر2 = س2 + ص2 حسب نظرية
فيثاغورس للمثلث القائم الزاوية. وأن (س) و(ص) لا يتغيران إذا أضيفت الزوايا
الدائرية (2 ط) على الزاوية، بمعنى أنه إذا أضيف 360ْ إلى الزاوية فإن جا (أ + 2 ط)
= جا أ ، وهناك عبارات أخرى تنطبق على الدوال الخمس الأخرى. وتعتبر ثلاثة من هذه
الدوال عكس الثلاثة الأخرى بمعنى أن:

ظتا أ = ظا أ / 1 ، قا أ = جتا أ / 1 ، قتا أ = جا أ / 1

وإذا كانت أ، ب، ج هي الزوايا الثلاثة لمثلث، وكانت س ص ع هي الأضلاع
المقابلة الخاصة بكل من هذه الزوايا، بالتالي يمكن إثبات أن:
جا أ / س = جا أ / ص = جا أ / ع

ويمكن أن تأخذ قوانين جيب التمام (جتا) والمماسات أشكالا أخرى بالتناوب بين
الحروف الزوايا (أ ب ج) والأضلاع (س ص ع).

ويمكن استخدام هذه العلاقات الثلاثة في حل أي مثلث بمعنى أنه يمكن الوصول
إلى الزوايا أوالأضلاع المجهولة عند معرفة: ضلع واحد وزاويتين، أو الضلعين والزاوية
المحصورة بينهما، أو ضلعين وزاوية مقابل أي منهما (عادة ما يكون هنالك مثلثان في
هذه الحالة) أو كل الأضلاع الثلاثة.

نبذة تاريخية

يعود تاريخ حساب المثلثات إلى أقدم ما دون عن الرياضيات في مصر وبابل، حيث
قاس البابليون الزوايا بالدرجات والدقائق والثواني. وحتى عصر اليونانيين، لم يوجد
أي تطور ملحوظ في حساب المثلثات، وفي القرن الثاني قبل الميلاد، وضع الفلكي
هيباركوس جدول مثلثي لحل المثلثات، حيث بدأ بــ 7.5ْ حتى وصل إلى 180ْ بدرجات
مقدارها 7.5ْ، وقد أعطى الجدول لكل زاوية طول الوتر المقابل لهذه الزاوية في دائرة
ذات نصف قطر ثابت ر. ومثل هذا الجدول مكافئ لجدول الجيب ، ولم تكن القيمة التي
استخدمها هيباركوس لنصف القطر (ر) محددة، ولكن بعد مضي 300 عام استخدم الفلكي
بطليموس (ر)= 60 لأن اليونانيين قد أخذوا نظام الأرقام الستينية البابلي.

وقد ذكر بطليموس في كتابه المجسطي جدول أوتار لدرجات النصف من صفر إلى 180ْ
وهي تعادل (3600 / 1 ) من الوحدة، كما أنه قد شرح أيضا طريقة عمله لجدول الأوتار
هذا، وفي عرضه للكتاب ذكر أمثلة عديدة على كيفية استخدام الجدول للتوصل إلى الأجزاء
المجهولة من المثلثات من خلال الأجزاء المعروفة، وقد ذكر بطليموس ما يعرف الآن باسم
نظرية مينيلوس لحل المثلثات الكروية، ولقرون عديدة كان ما دونه بطليموس في حساب
المثلثات المقدمة الأساسية للموضوعات التي يتناولها أي فلكي.

وفي نفس عصر بطليموس تقريبا، طور الهنود نظاما لحساب المثلثات يعتمد على
دالة الجيب وليس على دالة الوتر التي اعتمد عليها اليونانيون، وعلى عكس الدالة
الحديثة، لم تكن دالة الجيب هذه نسبة وإنما كانت ببساطة طول الضلع المقابل للزاوية
في مثلث قائم الزوايا ذي وتر ثابت محدد، هذا وقد استخدم الهنود قيما متعددة لوتر
المثلث القائم الزاوية.

وفي نهاية القرن الثاني الهجري / الثامن الميلادي، ورث الفلكيون المسلمون
التراث اليوناني والهندي واستخدموا دالة الجيب، وبحلول نهاية القرن الرابع الهجري /
العاشر الميلادي، كانوا قد أكملوا الجيب والدوال الخمس الأخرى، كما وضعوا العديد من
النظريات الأساسية في حساب المثلثات تتعلق بكل من المثلثات المستوية والكروية.

فقد رأى البيروني أن الفترات المتساوية بين الزوايا لا تقابلها تغيرات
متساوية في النسب المثلثية ، فأثبت صحتها بالطرق الهندسية، وقام بعمل جداول للجيب
لكل ربع درجة بدلا من الجداول المعروفة آنذاك، وقد قام بإيجاد طول الوتر في دائرة
يقابل زواية قدرها 40ْ عند المركز، وكان هدفه إيجاد الأوتار التي تقابل من الدورة
الكاملة ثلثها وربعها وخمسها، وقد تمكن من استنتاج قوانين مبسطة لحساب قيم هذه
الأوتار فيما عدا وتري السبع والتسع، كما استنتج قوانين لوتر مجموع زاويتين أو
الفرق بينهما أو قيمة نصف الزاوية مستخدما طريقة التقريب المتتابع.

ثم طور الطوسي من نظريات جيب الزاوية إلى ما هي عليه الآن مستعملا المثلث
المستوي، وعمل في ذلك الجداول الرياضية له ، كما قدم قاعدة الأشكال المتتامة وهي
الصورة المبسطة لقانون الجيوب الذي يقضي بأن جيوب الزوايا تتناسب مع الأضلاع
المقابلة لها.

أما الكاشي فقد حسب جداول جيب الدرجة الأولى، واستخدم ذلك في معادلة ذات
الدرجة الثالثة في معادلاته المثلثية ويقول في ذلك: " إذا علم جيب قوس، وأريد معرفة
جيب ثلاثة أمثالها، يضرب مكعب ذلك الجيب في أربع ثوان، وينقص الحاصل من ثلاثة
أمثاله، فالباقي هو الجيب المطلوب" وصورة ذلك على مايلي:
(جا 3س = 4جا س2 - 3جا س).

كما توصل المسلمون أيضا إلى المثلث القطبي للمثلثات الكروية، وقد طبقت كل
هذه الاكتشافات في أغراض فلكية، واستخدمت كوسيلة مساعدة في حساب الوقت فلكيا، وفي
التوصل إلى اتجاه مكة المكرمة لأداء الصلوات الخمس التي فرضتها الشريعة الإسلامية،
كما توصل العلماء المسلمون إلى جداول ذات دقة عالية، فعلى سبيل المثال الجداول التي
وضعوها للجيب والمماس كانت دقيقة جدا بنسبة أكبر من جزء واحد من 700 مليون.

وقد اهتم الطوسي بعلم حساب المثلثات الكروية اهتماما بالغا ووصل فيها شأوا،
فكان أول من قدم المتطابقات المثلثية للمثلث الكروي قائم الزاوية. أما ابن يونس فقد
ابتكر القانون المعروف في حساب المثلثات

(جتا أ جتا ب =2 / 1 [ جتا (أ + ب ) + جتا ( أ- ب)])

الذي يقضي بتحويل عملية الضرب إلى عملية جمع، فكان بذلك واضعا أول حجر في
تطوير علم اللوغاريتمات. ولقد اشتغل البتاني بالأعمال الفلكية الموجهة إلى حساب
المثلثات، وكان يستخدم الجيوب بانتظ ام مع يقين واضح من تفوقها على الأوتار التي
استعملها الإغريق من قبل. وقد أكمل إدخال دوال الظل وظل التمام، وعمل جدولا لظل
التمام بدلالة الدرجات على أساس العلاقة (ظتا أ = جتا أ / جا أ). كما عرف العلاقة
بين الأضلاع والزوايا في المثلث الكروي العام والتي يعبر عنها بالمعادلة


(جتا أ = جتاب. جتا جـ + جا ب. جا جـ).

وبعد ذلك، تعرف الغرب على ما صاغه المسلمون في علم حساب المثلثات من خلال
ترجمة كتب الفلك العربية وقد بدأت حركة الترجمة في القرن الثاني عشر، وقد كان أول
عمل غربي يكتب في هذا الموضوع من تأليف الفلكي والرياضي الألماني يوهان مولر وقد
سمى كتابه ريجيو مونتانوس .

وفي القرن التالي، توصل الفلكي الألماني جورج يوأخيم المعروف باسم ريتيكس
إلى المفهوم الحديث لدوال حساب المثلثات على أنها نسب وليست أطوال خطوط معينة. أما
الرياضي الفرنسي فرانسوا فيتي فقد أدخل المثلث القطبي في حساب المثلثات الكروية وقد
ذكر الصيغ المتعددة الزوايا للجيب وجيب التمام من خلال قدرة الجيب وجيب التمام.

وقد خطا حساب المثلثات خطوات كبيرة إلى الأمام في أوائل القرن السابع عشر
على يد عالم الرياضيات الأسكتلندي جون نابير الذي اخترع اللوغاريتمات، كما اخترع
أيضا بعض القوانين المساعدة للذاكرة لحل المثلثات الكروية وكذا بعض النسب لحل
المثلثات الكروية المائلة.

وبعد نصف قرن تقريبا من نشر نابير للوغاريتمات التي وضع أسسها ابن يونس،
توصل إسحاق نيوتن إلى حساب التفاضل والتكامل. وكان من ضمن الأساسيات التي اعتمد
عليها هذا العمل تقديم نيوتن للعديد من الدالات على أنها متسلسلات لا نهائية في
قدرات (س). ومن ثم فقد توصل نيوتن إلى متسلسلة الجيب (س) ومتسلسلة مماثلة لجيب
التمام (س) وظا (س). ومع اختراع حساب التفاضل والتكامل، أعيد النظر في تحليل الدوال
المثلثية حيث ما زالت تلعب دورا هاما في كل من الرياضيات البحتة والتطبيقية.

وأخيرا، وفي القرن الثامن عشر، عرف الرياضي السويسري ليونهارد يولر الدوال
المثلثية على أنها أعداد مركبة، وقد أدى هذا إلى أن جعل مادة حساب المثلثات بأكملها
تطبيقا واحدا من التطبيقات العملية الكثيرة للأعداد المركبة، وأظهر أن القوانين
الأساسية للرياضيات مجرد نتائج لحساب هذه الأعداد.

فيثاغورس {4}

{4}

فيثاغورس

ولد هذا المفكر حوالي عام 580 ق.م في جزيرة ساموس في بحر ايجه، باليونان، وجزيرة ساموس كانت إحدى المراكز التجارية المهمة في ذلك الوقت ، كما امتازت بثقافة مميزة.

وهذا أتاح لفيثاغورس، وهو ابن رجل ميسور، أن يتلقى أفضل تعليم ممكن آنذاك ، وحين بلغ السادسة عشرة من عمره بدأ يظهر نبوغه حتى عجز أساتذته عن الإجابة على أسئلته. لذا انتقل للتتلمذ على يد طالس الملطي، أول إغريقي أجرى دراسة عملية للإعداد.

أسس فيثاغورس مدرسته حوالي 529 ق.م في كروتونا، وهي ميناء إغريقي جنوب إيطاليا كان مزدهراً في تلك الحقبة، فالتحق بها عدد كبير من الطلاب. وكانت مدرسته أقرب لأن تكون فرقة دينية من أن تكون مدرسة بالمفهوم الصحيح للكلمة.

كان أعضاؤها يتعارفون بإشارة سرية، ويتشاركون في تملك جميع الأشياء، كما تعاهدوا على أن يعاون بعضهم بعضاً. تعرف نظرية فيثاغورس التي اقترنت باسمه، وتنص على أنه في المثلث قائم الزاوية، ويكون مربع الوتر، أي الضلع الأطول، مساوياً لمجموع مربعي الضلعين الآخرين.

واكتشف أيضاً مجموع الزوايا الثلاث لأي مثلث يساوي زاويتين قائمتين.

كما يعتقد بعضهم أنه هو الذي فكر في جدول الضرب المعروف، بالرغم من عدم وجود ما يثبت ذلك. افتتن فيثاغورس بالأرقام، وأشهر أقواله: (كل الأشياء أرقام).

وليس ذلك قولاً شاذاً، كما قد يبدو لأول وهلة، وأن كل شيء في العالم إنما يتكون من أعداد من الذرات مرتبة بأشكال مختلفة.

كان فيثاغورس يفكر أن الأعداد لها أشكال كالتي نراها في (زهر) الطاولة، وفكرة تسميته الأعداد (مربعة) أو (مكعبة) إنما هي فكرته هو.

لم يكن فيثاغورس مولعاً بالأعداد والهندسة فحسب وإنما بالعلوم الأخرى المعروفة، فضلاً عن شغفه بعلوم الدين لم تكن هناك كتب آنذاك منتشرة، فقد كانت الطريقة المفضلة لمواصلة الدراسة هي الارتجال ولقاء العلماء.

قضى فيثاغورس عدة أعوام في مصر. وفي الخمسين من عمره كان قد تعلم الكثير فأراد إنشاء مدرسة ليعلم الآخرين.

كانت دروس فيثاغورس تتناول درجات الحكمة الأربع:

الحساب، الهندسة، الموسيقى، الفلك، وواجبات الإنسان نحو الآخرين، والدين ، وكان يفرض على طلابه ممارسة فضائل المروءة والتقوى والطاعة والإخلاص، أي كل ما كان ينادي به المجتمع الإغريقي المثالي. الحياة النقية في رأي فيثاغورس، تعني حياة التقشف.

وهناك عدد من القواعد التي وضعها كانت أشبه بالطقوس الدينية وعلى سبيل المثال كان محظوراً على تلاميذه أن يقلبوا النار بقضيب من حديد، أو يلتقطوا ما وقع على الأرض، كانت الموسيقى لدى فيثاغورس ذات أهمية بالغة.

من تعاليم فيثاغورس أن الأرض والكون مستديران، ولهذا فإن التعليم المتكامل هو الذي يجمع بين الدراسة العلمية والقواعد الأخلاقية والدين.

كان تدريس فيثاغورس خليطاً من التصوف والتحليل العقلي.

وانغمس الفيثاغورسيون في السياسة، وكانوا كلما اكتسبوا مرتبة أو سلطاناً أظهروا الاحتقار للجماعات الجاهلة التي لا تستطيع أن تحيا حياة التأمل الرفيعة. وأدى ذلك إلى سقوطهم بعدما ثار الناس عليهم.

توفي فيثاغورس في الثمانين من عمره، وظلت تعاليمه ونظرياته تزداد انتشاراً !! بعد مائتي عام أقام مجلس الشعب (البرلمان) تمثالاً لفيثاغورس في روما تكريماً وتقديراً وعرفاناً بوصفه حكيماً إغريقيا كبيراً

ألاعداد النسبية {3}

{3}

الأعداد النسبية

التمهيد :

العدد +4 عدد موجب مسبوق بإشارة ( + ) . نُسمي العدد (
+4 ) عدد طبيعي .

العدد ( -4 ) هو سالب العدد ( +4 ) . يقابل كل عدد
طبيعي ( موجب ) عدد سالب يُسمى سالب العدد .

تُسمى الأعداد الطبيعية والأعداد السالبة المقابلة لها
والصفر بالأعداد الصحيحة .

العدد 5 عددٌ صحيح يُمكننا كتابته على صورة كسر بسطُهُ
عددٌ صحيح ( 5 ) ومقامُهُ عددٌ صحيح ( 1 )

نقول الكسر 1/5

بسطُهُ عددٌ صحيح ( 5 ) ومقامُهُ عددٌ صحيح ( 1 ).

الكسر 4/3

بسطُهُ عددٌ صحيح ( 3 ) ومقامُهُ عددٌ صحيح ( 4 ) .

وكذلك الكسر 4/-2

بسطُهُ عددٌ صحيح ( -2 ) ومقامُهُ عددٌ صحيح ( 4 ).

العدد النسبي

نُسمي العدد الذي يُمكن كتابته على صورة كسر بسطُهُ
عددٌ صحيح ومقامُهُ عددٌ صحيح بالعدد النسبي .

يُكتب العدد النسبي على الصُّورةِ ب/أ حيثُ
أ ، ب عددانِ صحيحانِ ، ب لا تساوي صفراً.

مجموعة الأعداد النسبية هي المجموعة التي تشتمل على جميع الأعداد النسبية ، ونستخدم
الرمز للدلالة عليها

إنتهى